数据结构与算法之美
Table of Contents
01 | 复杂度分析
时间复杂度
大 O 时间复杂度表示法: T(n)=O(f(n))
n 表示数据规模, T(n) 表示代码运行的耗时, f(n) 表示每行代码执行次数的总和,是一个公式, O 代表 T(n) 和 f(n) 成正比。
大 O 时间复杂度表示代码随规模增长的变化趋势,并不是真正的执行时间,所以叫 渐进时间复杂度(asymptotic time complexity) ,简称 时间复杂度 。
分析方法:
- 只关注循环次数最多的一段代码
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
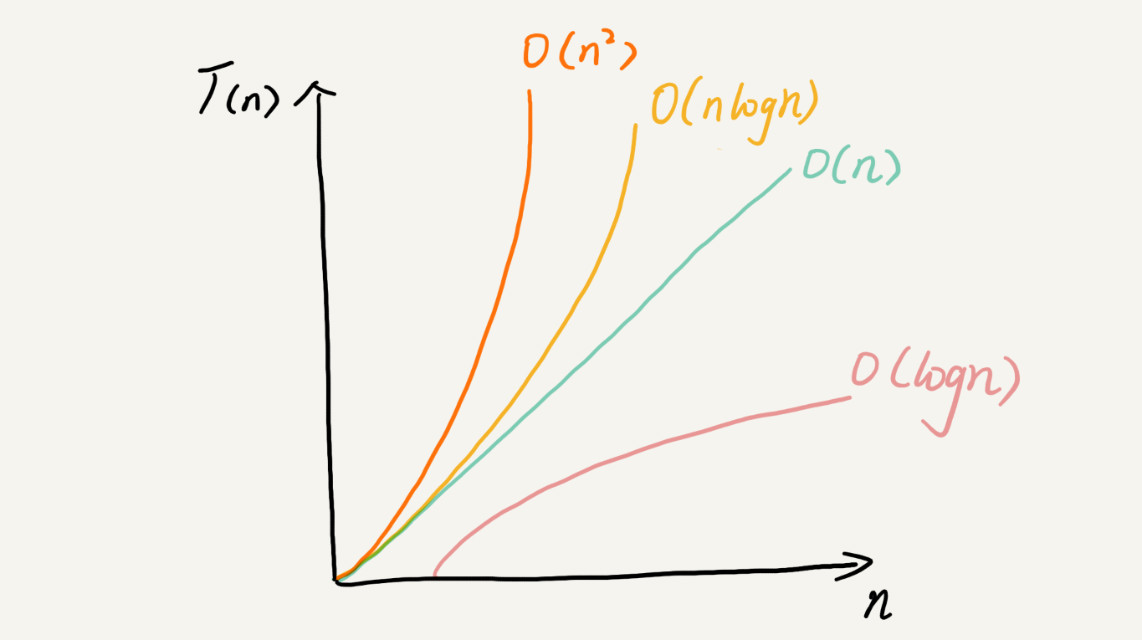
常见时间复杂度分析:

其中 O(\({2^n}\)) 和 O(n!) 为非多项式量级,其他为多项式量级。非多项式量级算法会随着规模 n 的增大,执行时间急剧增加,是非常低效的算法,我们主要 关注 多项式时间复杂度 :
O(1)
只要代码执行时间不随着 n 的增大而增长,时间复杂度即为
O(1),如果代码中不含有循环、递归等类型代码,成千上万行代码的时间复杂度也是O(1)O(logn)、O(nlogn)
i = 1 while i < n: i = i * 2
上面这个循环代码执行次数可以通过 2^x=n , 求得 x=log2n ,则时间复杂度为 O(log2n) ,如果换成 i * 3 ,那么时间复杂度为 O(log3n) ,
因为对数之间是可以相互转换的,所以可以忽略对数的“底”,统一表示为 O(logn)。O(nlogn) 自然就是循环嵌套了,O(nlogn) 也是一种比较常见的算法时间复杂度,
如归并排序、快速排序的时间复杂度都是 O(nlogn)。
- O(m+n)、O(m*n)
此类时间复杂度是由两个数据的规模决定的
def cal(m, n):
i = j = 1
sum1 = sum2 = 0
while(i < m):
sum1 += i
i++
while(j < n):
sum2 += j
j++
return sum1 + sum2
我们无法估计 m 和 n 的量级谁大,就不能简单地使用加法规则,忽略掉其中一个,所以算法复杂度为 O(m+n),如果是嵌套的,则乘法规则依然有效即时间复杂 度为 O(m*n)。
空间复杂度分析
空间复杂度全称 渐进空间复杂度(asymptotic space complexity) ,表示算法的存储空间和数据规模之间的增长关系。
可以粗略的估计,越高阶复杂度的算法,执行效率越低。 常见的复杂度从低阶到高阶: O(1)、O(logn)、O(n)、O(nlogn)、O(n2)
最好、最坏、平均、均摊时间复杂度
- 最好情况时间复杂度(best case time complexity) : 就是在最理想的情况下,执行代码的时间复杂度。
- 最坏情况时间复杂度(worst case time complexity) : 就是在最糟糕的情况下,执行代码的时间复杂度。
- 平均情况时间复杂度 : 全称应该叫做 加权平均时间复杂度 或者 *期望时间复杂度*。
- 均摊时间复杂度 : 对一组数据结构连续操作时,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,这些操作时间存在前后的时序关系,
这个时候可以尝试使用 摊还分析 (平摊分析),看能否将较高时间复杂度的耗时平摊到时间复杂度较低的操作上; *一般是可以使用均摊复杂度分析的场合,均摊时间复杂度=最好情况时间复杂度*。
02 | 数组:为什么很多编程语言中数组都从0开始编号?
如何实现随机访问?
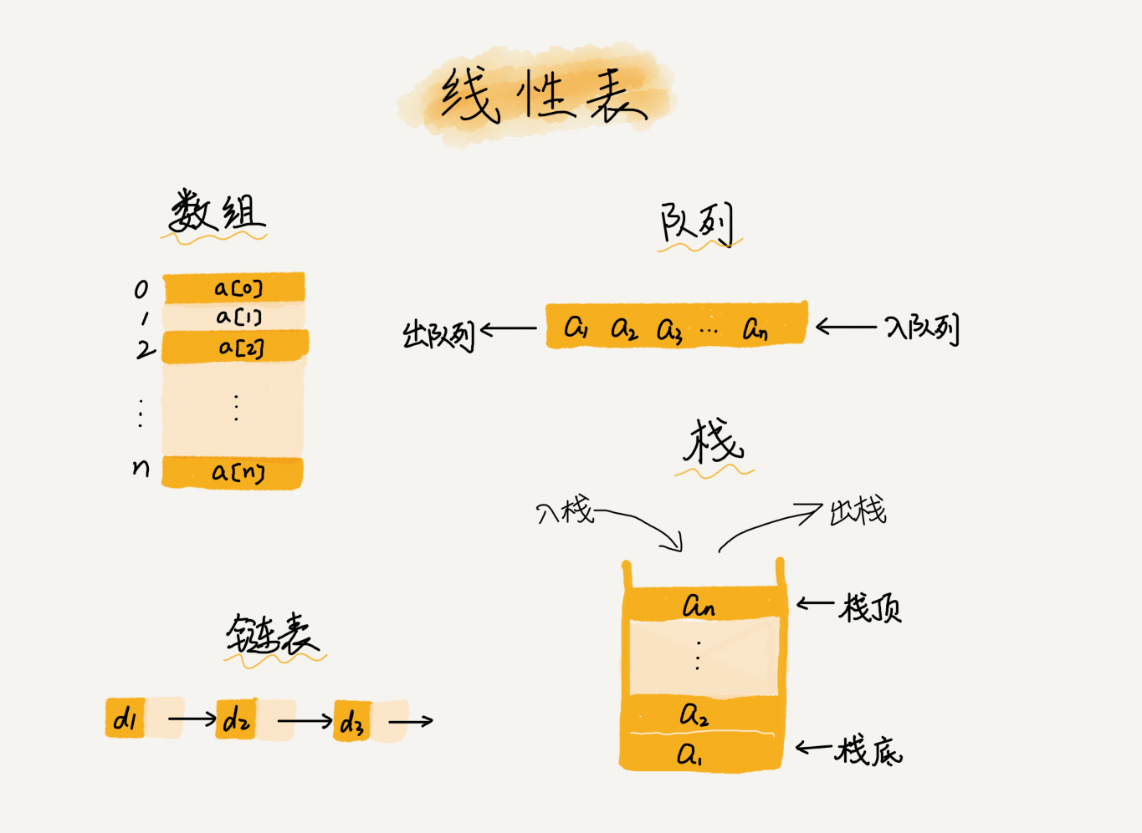
数组(Array)是一种线性表数据结构,用一组连续的内存空间,来存储一组具有相同类型的数据 。
定义中的几个概念:
- 线性表:数据排列像“线”一样的结构,只有前后两个方向,如数组、栈、队列、链表等
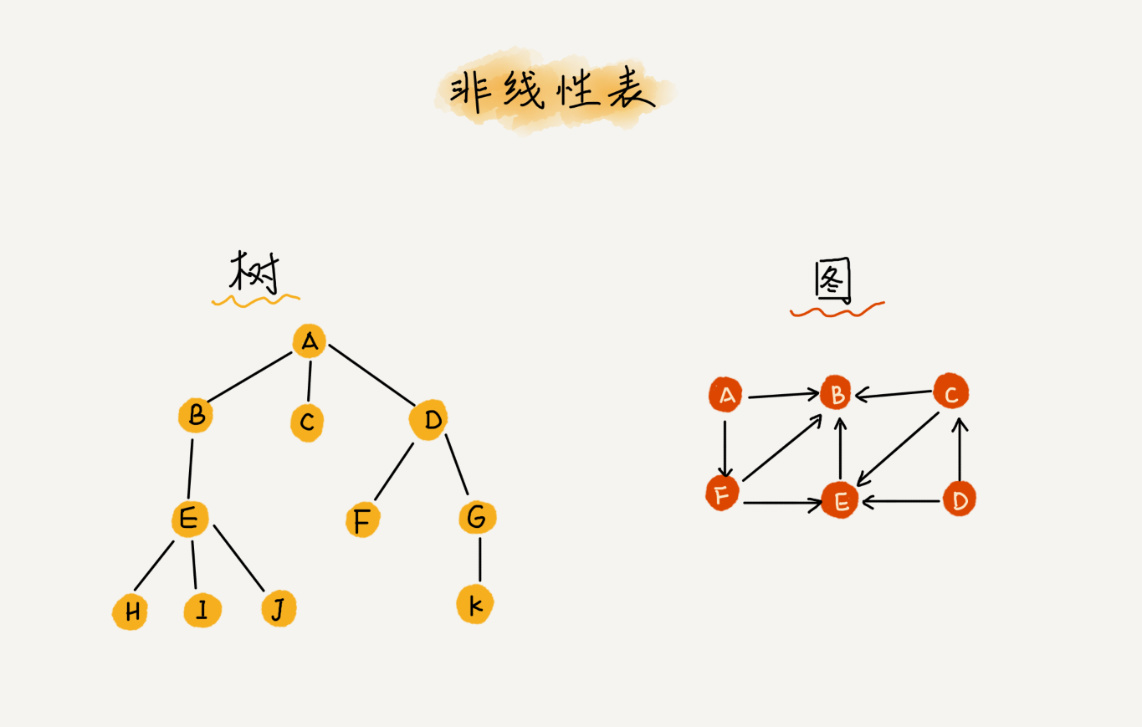
- 非线性表: 数据之间不是简单的前后关系,如:树、堆、图等
- 连续的存储空间和相同的数据类型:正是因为这两点,数组才具备了“杀手锏”的特性:随机访问。
以长度为10的数组为例 int[] a = new int[10] ,内存块的首地址为 base_address=1000
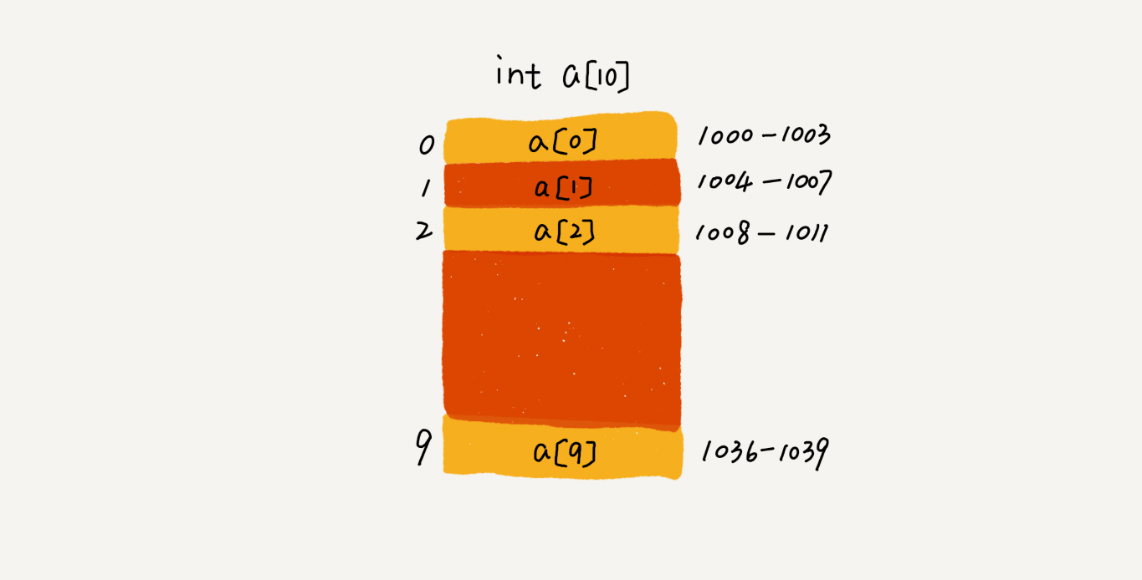
计算机会给每个内存单元分配地址,通过地址来访问内存中的数据,寻址公式: a[i]_address = base_address + i * data_type_size 。
数组适合查找操作,但时间复杂度不是 O(1),即使是排好序的数据,使用二分查找,时间复杂度也是 O(logn),所以,准确的表述应该是: *数组支持随机访问,根据下标随机访问的时间复杂度为 O(1)*。
数组的插入和删除,最好情况时间复杂度为 O(1) 即从末尾插入或删除元素;最坏时间复杂度为 O(n) 即从开头插入或删除元素,平均时间复杂度为 O(n),
所以 a[k]_address = base_address + k * type_size ,而如果数组从 1 开始,那么 a[k]_address = base_address + (k-1) * type_size
有大量的搬移操作。
数组为什么要从 0 开始
从数组的存储模型上来看,“下标”最确切的定义应该是“偏移(offset)”, a[0] 就是偏移为 0 的位置,a[k] 表示偏移 k 个 type_size,
所以 =a[k]_address = base_address + k * type_size ,而如果数组从 1 开始,那么 a[k]_address = base_address + (k-1) * type_size ,
每次随机访问数组,多了一次减法运算,对 cpu 来说就多了一次减法指令,数组作为基础的数据结构,随机访问又是基础操作,所以效率的优化需要
做到极致。当然也有可能是 C 语言使用 0 作为数组下标的开始,其他语言纷纷效仿。
03 | 链表
链表和数组的区别
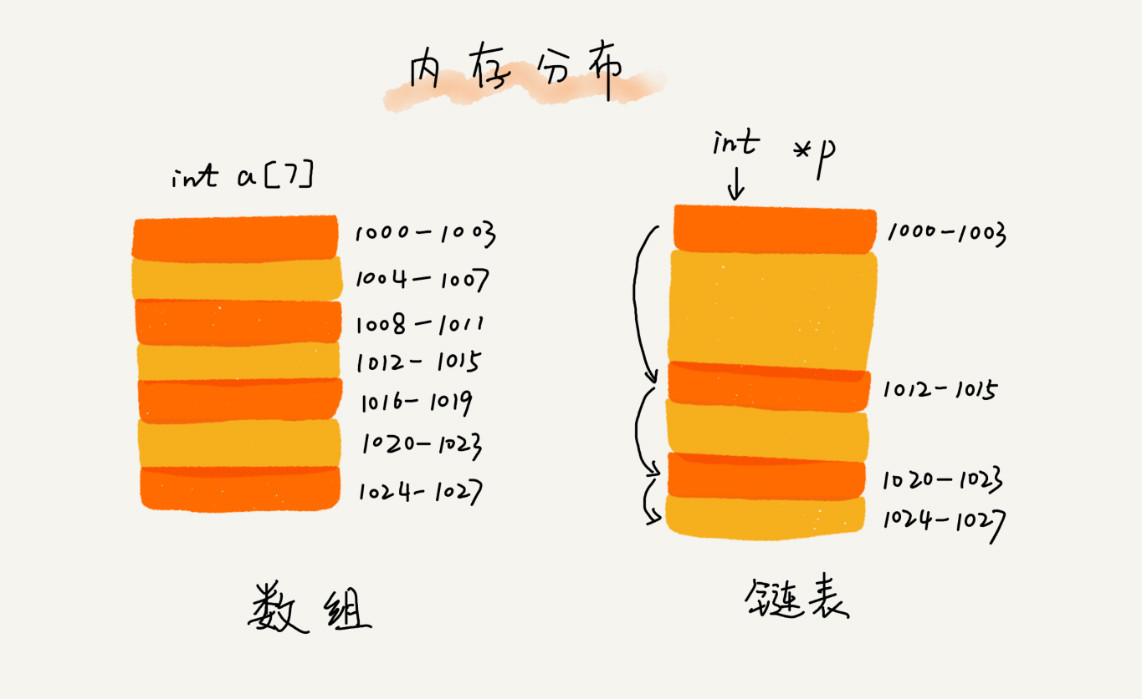
数据分配的存储空间需要是连续的,而链表则不需要连续。
链表分类
单链表
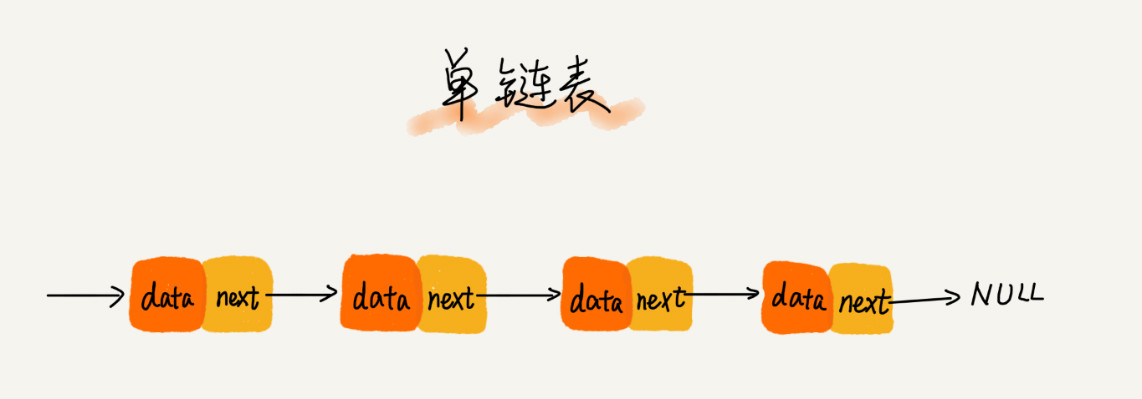
链表的节点除了要存储数据之外还要记录下一个节点的地址,我们称之为后继指针 next 。第一个节点称为 头节点 , 记录链接的开始地址,最后一个节点称为 尾结点 ,尾结点的下个地址指向空地址 NULL。
链表的插入和删除*操作*时间复杂度为 O(1),但查询需要遍历整个链表,所以时间复杂度为 O(n)。
循环链表
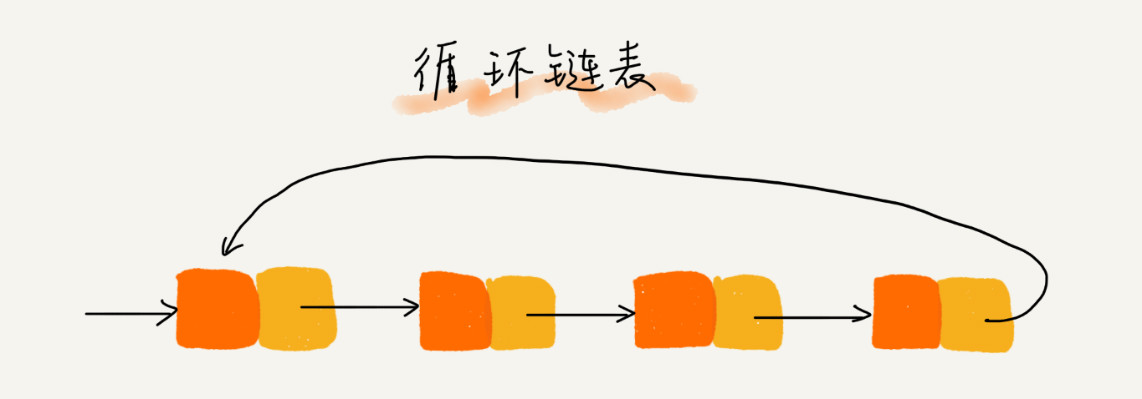
循环链表,首尾相连,是和处理具有环形结构特点的数据
双向链表
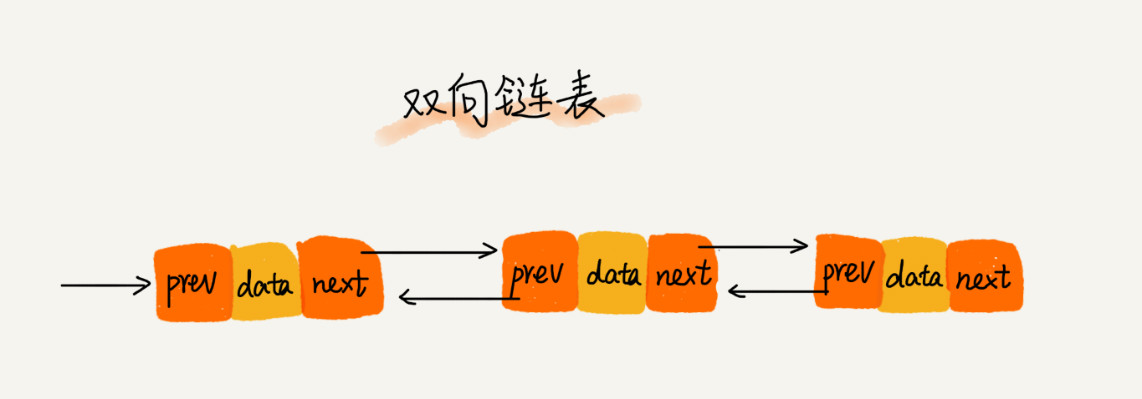
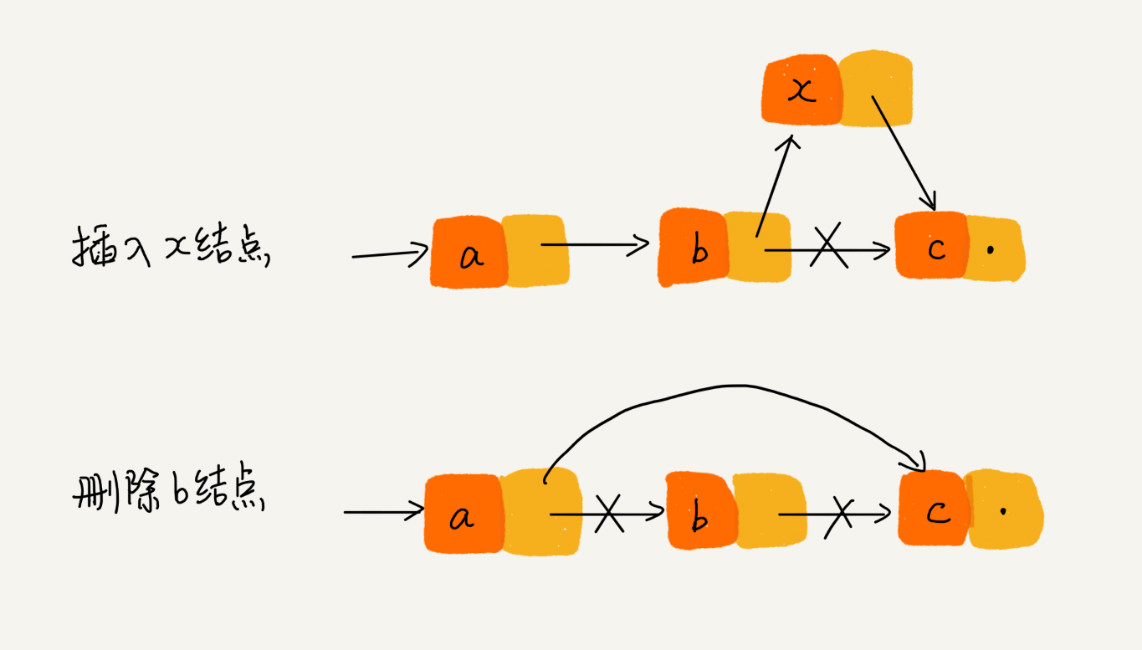
单链表只有一个方向,双向链表存储后继指针 next 的同时,还有一个前驱指针 prev ,所以数据相同时,双向链表会消耗更多的存储空间。 但双向链表支持双向遍历,在特定情况下,双向链表的插入、删除操作比单链表更高效。
以删除操作举例:
- 1. 删除节点中“值等于给定值”的节点
- 2. 删除给定指针指向的节点
对于第一种情况,单链表和双向链表都需要遍历整个链表,找到对应节点进行删除,尽管 删除 操作本身的时间复杂度为 O(1),但遍历查找的时间复杂度为 O(n),
所以时间复杂度为 O(n);
对于第二种情况,因为双向链表存储了前驱指针,所以可以直接删除,时间复杂度为 O(1)。但单链表还需要遍历,直到 p-next = q ,说明p是q的前驱节点,才能删除,所以时间复杂度仍为 O(n)。
如何基于链表实现 LRU 缓存淘汰算法?
我们可以维护一个有序的单链表,越早访问的节点越靠近尾部。
当有一个新数据访问时,遍历单链表,
如果命中,把对应节点从原位置中删除,再重新插入到链表头部。
如果没有命中,将节点插入到链表头部,需要区分两种情况:
- 链表已满,需要删除最后一个节点,并将新节点插入到头部
- 链表未满,直接将新节点插入到头部
无论链表满没满,都需要遍历链表,所以时间复杂度为 O(n)。
如何轻松写出正确的链表代码?
技巧一:理解指针或引用的含义
不管指针还是引用,其实就是只存储数据的内存地址 。
将某个变量赋值给指针,实际上是将这个变量的地址赋值给指针,或者说,指针存储了这个变量的内存地址,通过指针可以找到这个变量。
如:
p->next = q ,是指 p 节点中的 next 指针存储了 q 的地址
p-next = p->next->next , 是指 p 节点的 next 指针存储了 p 节点下下个节点地址
技巧二:警惕指针丢失和内存泄露
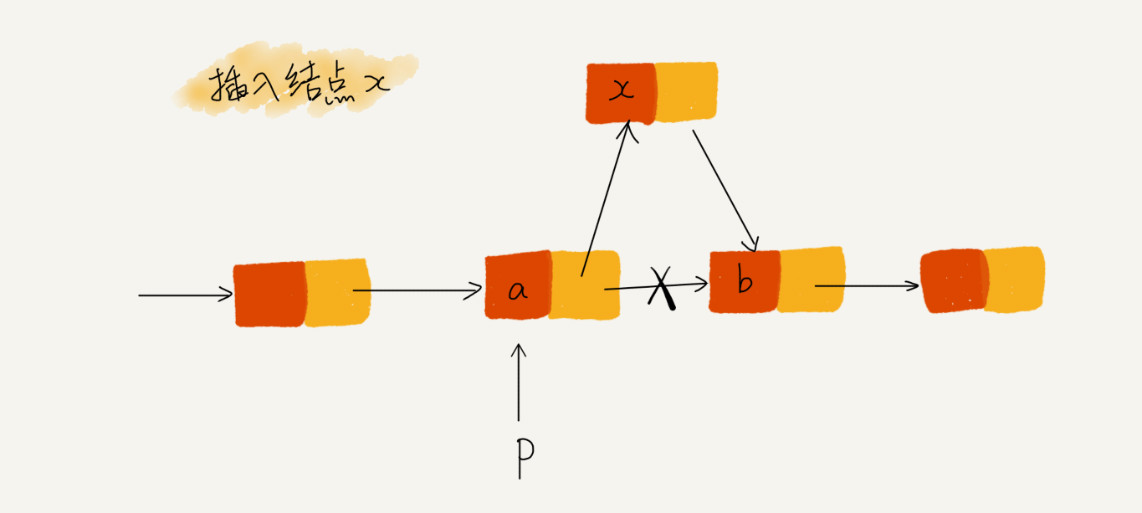
技巧三:利用哨兵简化实现难度
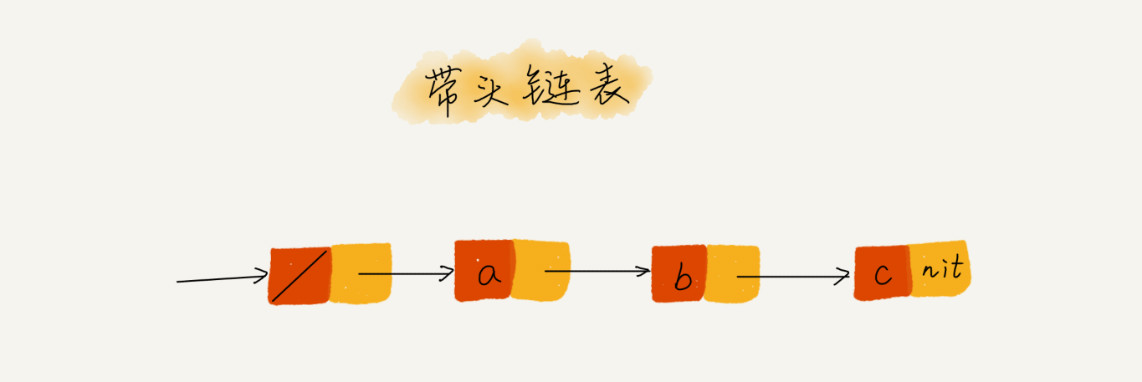
针对链表的插入、删除操作,需要对第一个节点的插入和最后一个节点的删除进行特殊处理,可以引入*哨兵节点*,不管链表是否为空,head指针会一直指向哨兵节点, 带哨兵节点的链表称作带头链表。
技巧四:重点留意边界条件
检查边界条件是否考虑全面,如:
- 如果链表为空,是否能正常工作
- 如果链表只包含一个节点或者两个节点,是否正常工作
- 代码逻辑再处理头、尾节点时是否正常工作
技巧五:举例画图,辅助思考
技巧六:多谢多练,没有捷径
- 单链表翻转
- 链表中环的检测
- 删除链表倒数第n个节点
- 求链表的中间节点